2023年12月12日
今日の活動
高校ぐらいからよく寝ると次の日の体感寒さが寝不足のときよりマシという経験を持っている。
11月より今月はよく寝ているので、いやあ今日もよく寝たから寒くないなあ!と思ってたのだが、もしかして、普通に今11月より暖かいか?
今日のわんこ
家帰って玄関をあけた瞬間、リビングから飛び出てきた。外でられるとマズイと思って臨戦態勢を取ったが、ちゃんと土間に降りる前に立ち止まった。えらいぞ。
今日のアークナイツ
やっと今回のイベント理解した。
Advent Calendar 12日目
おさらい。ちょっとずつ伸びた。
\([a_0, a_1, a_2] + [b_0, b_1, b_2] = [a_0+b_0, a_1+b_1, a_2+b_2]\)
\(t[a_0, a_1, a_2] = [ta_0, ta_1, ta_2]\)
\([a_0, a_1, a_2] \times [b_0, b_1, b_2] = [a_0b_0, a_1b_0+a_0b_1, a_2b_0+a_1b_1+a_0b_2]\)
さて、このかけ算をn項にしてプログラムを書きたい。\([a_0b_0, a_1b_0+a_0b_1, a_2b_0+a_1b_1+a_0b_2]\)について、0番目の各項の添え字が(0,0)、1番目の各項の添え字が(1,0),(0,1)、2番目は(2,0),(1,1),(0,2)となっていて、()の中身の和がn番目と等しいということは使えそうだ。
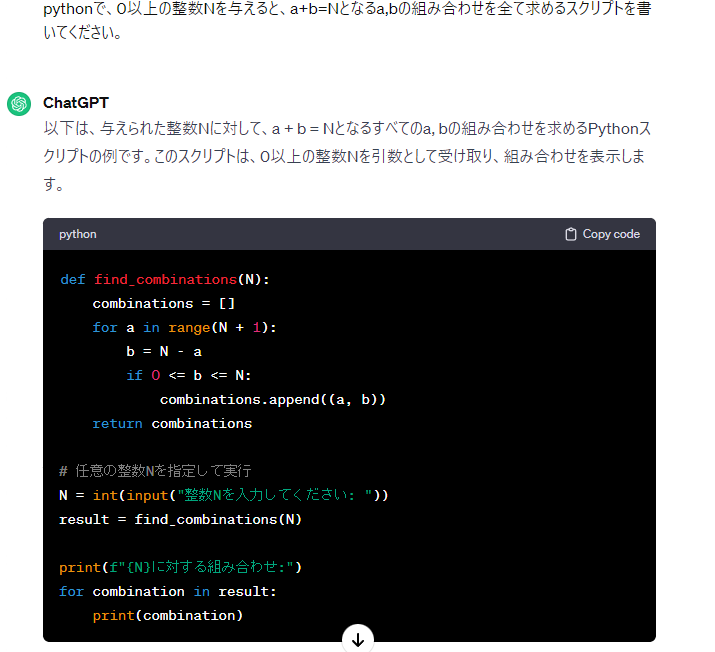
いや、流石にappendはしんどい。
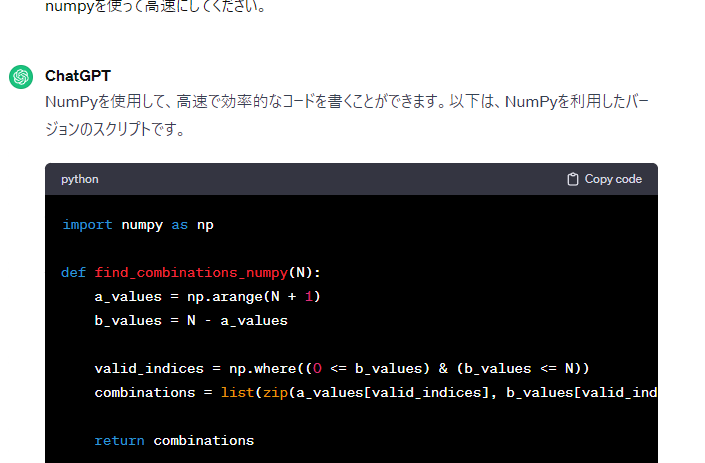
うむ。これを使おう
加減乗まではこんな感じ。まだ除やsin,cosはない。
import numpy as np
class MyClass:
def __init__(self, arr):
self.arr = np.array(arr)
def __repr__(self):
return repr(self.arr)
def __add__(self, other):
if isinstance(other, MyClass):
return MyClass(self.arr + other.arr)
else:
new_arr = self.arr.copy()
new_arr[0] += other
return MyClass(new_arr)
def __radd__(self, other):
return self.__add__(other)
def __mul__(self, other):
if isinstance(other, MyClass):
new_arr = [i for i in range(len(self.arr))]
for i in new_arr:
new_arr[i] = np.sum([self.arr[a] * other.arr[b] for a, b in _multiple_combinations(i)])
return MyClass(new_arr)
else:
return MyClass(self.arr * other)
def __rmul__(self, other):
return self.__mul__(other)
def __neg__(self):
return -1 * MyClass(self.arr)
def __sub__(self, other):
return self + (-other)
def __rsub__(self, other):
return -self + other
def _multiple_combinations(N):
a_values = np.arange(N + 1)
b_values = N - a_values
valid_indices = np.where((0 <= b_values) & (b_values <= N))
combinations = zip(a_values[valid_indices], b_values[valid_indices])
return combinations
multiple_comibnationsはclassの外にいた方がよい。MyClass.arrに依存しないものは積極的に外に出しておいたほうが、使い勝手がいい。
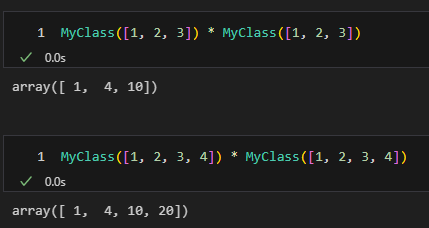
とりあえず実装はできていそうだ。
はて、今日はかけ算だけに留めよう。累乗だ。
# さっきの続き。
def __pow__(self, other):
newClass = MyClass(self.arr)
for i in range(other - 1):
newClass = newClass * self
return newClass

おお、それっぽい。それにしても累乗があると数字が一気に増えるな。

おや、1個目の数字を0にすると、かけ算の度に0がちょっとずつ浸食していくぞ??この様子だと、arrの長さがnのとき、n乗すると全て0になる気配がある。
気になる場合は上に示した3項のかけ算で累乗を手で計算して、実際に0が広がる様子を確認してもらうとよい。
この性質は明日さっそく割り算の定義で使いそうな気がするな~。
コメントを投稿
注意事項- 承認を受けるまでコメントは公開されません。
- 非公開を希望した場合、コメントは公開されません。
