2023年12月13日
今日の活動
今日からはじまったけど、みんなは参加した?僕は今日行きたいものあったんだけど、外せない業務があったから行けなかったけど。
今日のわんこ
帰ってくるの遅かったから、それまでちょっと寝てたっぽい。人間かって思っちゃうぐらいの伸びと声がでてた。
Advent Calendar 13日目
家帰ってからテイラー展開について考えてるの流石に疲れてきた。
おさらい。長さnのかけ算については12月12日の記事参照。
\([a_0, a_1, a_2] + [b_0, b_1, b_2] = [a_0+b_0, a_1+b_1, a_2+b_2]\)
\(t[a_0, a_1, a_2] = [ta_0, ta_1, ta_2]\)
\([a_0, a_1, a_2] \times [b_0, b_1, b_2] = [a_0b_0, a_1b_0+a_0b_1, a_2b_0+a_1b_1+a_0b_2]\)
- 配列の長さがnで、配列の最初が0のとき、n乗すると0になる
長さが2のときは割り算やルートを同じ日にやったけど、結構ボリュームあったので今日は割り算だけにしたい。
長さが2のときは全部計算して方程式で解いたが、長さがnのときはテイラー展開を利用したい。
\( \frac{1}{a+x} = \frac{1}{a} - \frac{x}{a^2} + \frac{x^2}{a^3} \cdots\)
この式を使う。一般化すると
\( \frac{1}{a+x} = \frac{1}{a} + \Sigma_{k=1}^{\infty}\frac{(-x)^k}{a^{k+1}}\)
こんな感じか。さて、長さが2のときに\(\sin\)でやったときのように\(x\)に\([a_0, a_1, \cdots, a_{n-1}]\)を代入する(長さがnとするためには最後の添え字はn-1だ。)。続けて\([a_0, 0, \cdots 0] + [0, a_1, \cdots a_{n-1}]\)と変換する。
\( \frac{1}{[a_0, a_1, \cdots, a_{n-1}]} = \frac{1}{[a_0, 0, 0, \cdots, 0] + [0, a_1, \cdots, a_{n-1}]}\)
\( = \frac{1}{[a_0, 0, \cdots, 0]} + \Sigma_{k=1}^{\infty}\frac{[0, a_1, \cdots, a_{n-1}]}{a_0^{k+1}}\)
ここで、"配列の長さがnで、配列の最初が0のとき、n乗すると0になる"を利用すると、\(\infty\)まで計算しなくとも、\(n-1\)乗まで計算すれば良いことに気づく。
\( = \frac{1}{[a_0, 0, \cdots, 0]} + \Sigma_{k=1}^{n-1}\frac{(-[0, a_1, \cdots, a_{n-1}])^k}{a_0^{k+1}}\)
\(n=2\)のとき
\( = \frac{1}{[a_0, 0]} + \frac{-[0, a_1]}{a_0^{2}}\)
\( = [\frac{1}{a_0}, \frac{-a_1}{a_0^2}]\)
前に示したものと同じだ。
\(n=3\)のとき
\( = \frac{1}{[a_0, 0, 0]} + \frac{-[0, a_1, a_2]}{a_0^{2}} + \frac{[0, a_1, a_2]^2}{a_0^{3}}\)
\( = [\frac{1}{a_0}, \frac{-a_1}{a_0^2}, \frac{-a_2}{a_0^2} + \frac{[0, a_1, a_2]^2}{a_0^{3}}]\)
\( = [\frac{1}{a_0}, \frac{-a_1}{a_0^2}, \frac{-a_2}{a_0^2} + \frac{[0, 0, a_1^2]}{a_0^{3}}]\)
\( = [\frac{1}{a_0}, \frac{-a_1}{a_0^2}, \frac{-a_0a_2+a_1^2}{a_0^3}]\)
頑張って[2, 3, 4]に対して手計算した。
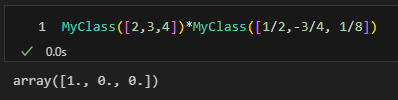
合ってそうだ。
じゃあまたコードにしよう。この\([a_0, 0, \cdots 0] + [0, a_1, \cdots a_{n-1}]\)と変換するのは今後もやるので、今のうちに関数にしておく。
# 前回powの続きから
def _divided_differences(self):
r_arr = np.zeros(len(self.arr))
r_arr[0] = self.arr[0]
r_MyClass = MyClass(r_arr)
d_arr = self.arr.copy()
d_arr[0] = 0
d_MyClass = MyClass(d_arr)
return r_MyClass, d_MyClass
def inverse(self):
new_MyClass, d_MyClass = self._divided_differences()
new_MyClass.arr[0] = 1/new_MyClass.arr[0]
for i in range(1, len(self.arr)):
new_MyClass = new_MyClass + ((-1)**i/self.arr[0]**(i+1))*(d_MyClass**i)
return new_MyClass

できてそうだ。もし、このコードを使ってすごく計算が大変なことをしたい場合、inverse関数のd_MyClass**iはforループのiが増える度に最初から計算する仕様になっているので工夫を考えた方が良い。
この考えを導入したい理由が、物理をやる時にn次のテイラー展開した式を考えると~とやる場合のnは所詮大きな数にならないと思う(高校物理は1次までだったもんね)のだが、とあることを考えると一気に計算が大変になる。
帰宅してからテイラー展開の式を見てipynbファイルを開きながらつくっているので割り算だけでもかなりFF14の時間削ってるのだ、許してくれ。
コメントを投稿
注意事項- 承認を受けるまでコメントは公開されません。
- 非公開を希望した場合、コメントは公開されません。
