2023年12月20日
今日の活動
寝不足の気配を感じる
今日のわんこ
毛をとかしてる間、ひたすらキバむき出しで耐えてた。
Advent Calendar 20日目
微分も積分もできた。じゃあ最後は微分方程式だ。
\(y'(x) = y\)となる微分方程式を考える。また初期値は\(y(0)=1\)とする。
ここではとりあえず、\(x=1\)の結果がわかれば十分としよう。解析的な考えだと実数全体で知りたいとかあるのだろうが、数値的にわかれば十分というケースも多い。そりゃ解析的な答えが分かるに越したことはないが、分からんのだ。
先にいうと答えはモチロン\(y(x)=e^x\)なので、\(y(1)=e\)が知りたい答えである。つまり、2.718ぐらい。
オイラー法だとこうか。
\(y(0+\Delta x) = y(0) + y'(0)\Delta x\)となる。ここで、\(\Delta x = 1\)とすると
\(y(0+1) = y(0) + y'(0)\)
\(y(1) = y(0) + y(0)\)
\(y(1) = 2\)
整数は合ってるが、流石に2.7と比較すると小さい気がする。\(\Delta x = 1\)とした時点でこんな精度だろう。せめて0.5にする。
\(y(0.5) = y(0) + y'(0)\times 0.5\)より
\(y(0.5) = 1.5\)となる。
\(y(0.5 + \Delta x) = 1.5 + y'(0.5)\Delta x\)
\(y(1) = 1.5 + 1.5\times 0.5\)
\(y(1) = 1.5 + 0.75 = 2.25\)
うーん、4回にわけるか。
\(y(0.25) = y(0) + y(0)/4 = 1.25\)
\(y(0.5) = y(0.25) + y(0.25)/4 = 1.25 + 1.25/4 = 1.5625\)
\(y(0.75) = y(0.5) + y(0.5)/4 = 1.5625 \times 5/4 = 1.953125\)
\(y(1) = 1.953125 \times 5/4 = 2.44140625\)
知りたい答えは2.718ぐらいなのだが、100回にわけてもまだ2.704ぐらいで2.71には遠い。数値解を求めるのも大変である。
4次のルンゲクッタ法だとこうか。\(dy/dx = f(x, y)\)とした場合、今回は\(f(x, y) = y\)となるので、
\(k_1 = f(0, y(0)) = y(0) = 1\)
\(k_2 = f(0+\Delta x/2, y(0)+\Delta x /2 \cdot k_1) = y(0)+ k_1 / 2 = 1.5\)
\(k_3 = f(0+\Delta x/2, y(0)+\Delta x /2 \cdot k_2) = 1.75\)
\(k_4 = f(0+\Delta x, y(0)+\Delta x \cdot k_3) = 2.75\)
\(y(1) = y(0) + \Delta x \cdot (1+2 \cdot 1.5+2 \cdot 1.75+2.75)/6 = 2.708\)
あってる?てか一発でこんなに精度いいの?むしろ僕のオイラー法があってる?
ちなみにscipy使っていいならこう。僕の手計算より2.718に近い。確かデフォルトのメソッドがRK45でorderが5(4)だからその差か?
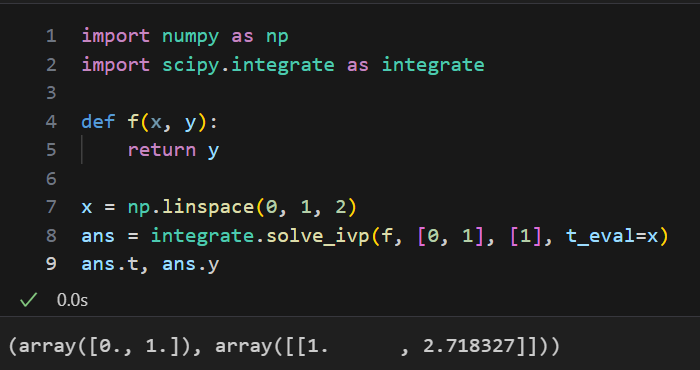
本当に申し訳ないが、ゲームをしないといけない時間になった。オイラー法とルンゲクッタ法の手計算と検算に1時間かかるのは予想してなかった。
明日はMyClassを使って解く様子を紹介して大団円で終わろう。
コメントを投稿
注意事項- 承認を受けるまでコメントは公開されません。
- 非公開を希望した場合、コメントは公開されません。
