2023年12月18日
昨日の活動
XのAPIのアカウントが違った理由が解決したから、多分、このブログの告知は思った通りのアカウントで実施される。
週末のわんこ
妻に怒られるとき、僕の後ろに隠れるようになった。
Advent Calendar 18日目
もう少しわけることはできる気がしてきた。クリスマスは明日か明後日。
おさらい。え?Xしか見てなかったから何やってるのかわからないって?あのXに未だに頼ってばかりいる自分の日常を恥じろ!お前がそんなんでいるから新しいSNSの覇権が決まらないんだ!
追いかけるつもりがあるなら12/4から読むのが良い。12/1は今となってはどうでもいい話だ。
話が脱線した、[]付き演算記号の定義である。
\([a_0, a_1, a_2] + [b_0, b_1, b_2] = [a_0+b_0, a_1+b_1, a_2+b_2]\)
\(t[a_0, a_1, a_2] = [ta_0, ta_1, ta_2]\)
\([a_0, a_1, a_2] \times [b_0, b_1, b_2] = [a_0b_0, a_1b_0+a_0b_1, a_2b_0+a_1b_1+a_0b_2]\)
\(1/[a_0, a_1, a_2]= [\frac{1}{a_0}, \frac{-a_1}{a_0^2}, \frac{-a_0a_2+a_1^2}{a_0^3}]\)
\(f([a, 1]) = [f(a), f'(a)]\)
- 配列の長さがnで、配列の最初が0のとき、n乗すると0になる
12/5の記事、\(f(x) = \frac{x}{1/x+2}\)としたときについて改めて考える。おさらいにも書いたが、\(x=[2, 1]\)とするとf(2)とf'(2)の結果が同時に得られたのが当時の話だった。
今回は\(f(2), f'(2), f''(2), f'''(2), f^{(4)}(2)\)まで考えよう。そういや毎回こうやってスクリーンショットアップロードするのかったるいんだけどなんか良い方法ないんかね?
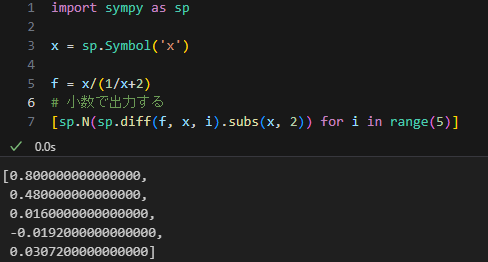
今まで作成してきたMyClassで計算するとこうなる。

まず、これを計算するときは[2, 1, 0, 0, 0]を代入すれば十分である。[2, 1, 1, 0, 0]とかではない。その上で3つめの数値からずれていることがわかる。
これは12/11の記事で
\(f(x) = f(x_o) + f'(x_o)(x-x_o) + \frac{f''(x_o)}{2!}(x - x_o)^2 + \cdots \)を
\(f(x) = a_0 + a_1(x-x_o) + a_2(x - x_o)^2 + \cdots \)としたことに起因する。
このブログで実施したかけ算の定義ではテイラー展開で出てくる階乗分の1を含んでしまっている。よって、12/5当時書いた長さが2のときは\(f([a, 1]) = [f(a), f'(a)] = [f(a), \frac{1}{1!}f'(a)]\)となっていた。
よって、配列の長さが伸びると\(f([a, 1, 0]) = [f(a), \frac{1}{1!}f'(a), \frac{1}{2!}f''(a)]\)と、実際の微分係数を階乗分の1倍した値が出てくる。そのため、sympyで出てきた数値を階乗分の1してあげると
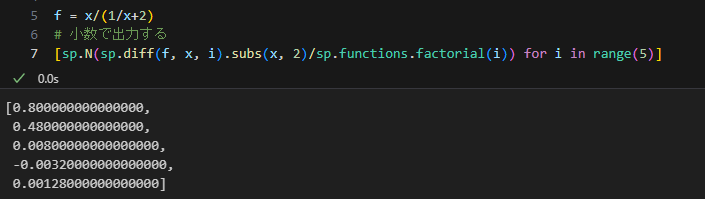
MyClassの計算と同じになる。これで簡単な関数ならMyClassを使って微分係数を求めることができるようになったよ、よかったね。
よかったねと書いたが、このMyClassを使ってやりたいことは、「テイラー展開した係数を[]の中に並べて、約束通りに計算したら、テイラー展開された式を求めることができる」ということであり、微分係数が求まることはおまけである。が、多分テイラー展開された式を求めることに興味のない読者にやりたいことをわかった気にさせるにはコレが手っ取り早いと思う。
あと、sympyで階乗をどう書くのか調べるの面倒だったのだが、念じることでCopilotが空気読んでくれた。助かる。
コメントを投稿
注意事項- 承認を受けるまでコメントは公開されません。
- 非公開を希望した場合、コメントは公開されません。
