2023年12月8日
今日の活動
銀行のワンタイムパスワードカードの電池がLoになってたのでアプリに切り替えた。いつもスマホから銀行のあれこれやってんのにワンタイムパスワード機能をスマホに持たせるの意味わからなくね?って思うんだが、まあ生体認証を信じて自分のスマホを盗まれないことを祈るしかないのか。
まあ流石にワンタイムパスワードの再発行の方がだるい。
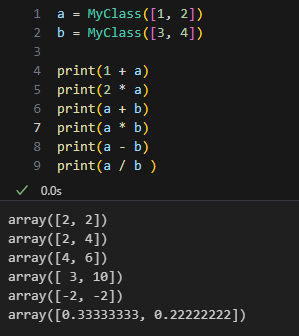
今日のわんこ
家の近くに車が止まるのにほんと敏感だなあと感心する。人間からしたらなんで吠えはじめたのか理解できないのだが、数分後に車のドアを閉める音が聞こえてようやく理解できる。
今日の夕食
肉
Advent Calendar 8日目
おさらいのコーナー。昨日は\(\sin{[a, 1]}\)だったけど\([a, b]\)に書き換えちゃうよ。
\([a, b] + [c, d] = [a+b, c+d]\)
\(t \times [a, b] = [ta, tb]\)
\([a, b] \times [c, d] = [ac, ad+bc]\)
\(1/[a, b] = [1/a, -b/a^2] \)
\(\sqrt{[a, b]} = [\sqrt{a}, \frac{b}{2\sqrt{a}}]\)
\(\sin{[a, b]} = [\sin{a}, b\cos{a}]\)
\(\cos{[a, b]} = [\cos{a}, -b\sin{a}]\)
とりあえず、これだけ出そろえば、関数同士の計算がテイラー展開を介さなくてもできるようになる。
\(\sin{[a, b]} \times \cos{[a, b]} = [\sin{a}, b\cos{a}] \times [\cos{a}, -b\sin{a}]\)
\(= [\sin{a}\cos{a}, b\cos{a}\cos{a}-b\sin{a}\sin{a}] \)
\(b\)が1なら、やはりこれは\(\sin{a}\cos{a}\)の微分係数を求めていることになる。
散々演算記号で遊んできたけど、これの何が嬉しいかというと、「この程度の計算ならなんかプログラム作れそうな気がする!」っていうことなのだ。
とりあえず四則演算はこんな感じになるはず。
import numpy as np
class MyClass:
def __init__(self, arr):
self.arr = np.array(arr)
def __repr__(self):
return repr(self.arr)
def __add__(self, other):
if isinstance(other, MyClass):
return MyClass(self.arr + other.arr)
else:
new_arr = self.arr.copy()
new_arr[0] += other
return MyClass(new_arr)
def __radd__(self, other):
return self.__add__(other)
def __mul__(self, other):
if isinstance(other, MyClass):
new_arr = [self.arr[0]*other.arr[0], self.arr[0]*other.arr[1] + self.arr[1]*other.arr[0]]
return MyClass(new_arr)
else:
return MyClass(self.arr * other)
def __rmul__(self, other):
return self.__mul__(other)
def __neg__(self):
return -1 * MyClass(self.arr)
def __sub__(self, other):
return self + (-other)
def __rsub__(self, other):
return -self + other
def __truediv__(self, other):
new_arr = [1/other.arr[0], -other.arr[1]/(other.arr[0]**2)]
return MyClass(self.arr) * MyClass(new_arr)
def __rtruediv__(self, other):
return MyClass(self.arr) / MyClass(other)
pythonで__add__とかの存在は確かに知ってはいたが、まさか自分で使うときがくるとは思ってもなかったんだな。ちなみに__radd__も定義しないと1+MyClassが計算できない。
はて、お次は\(\sin, \cos\)なのだが、np.sinが適用されたときに返す値を弄ることができるらしい。
class MyClass:
#さっきの__rtruediv__の続き
def __array__(self):
return self.arr
def __array_wrap__(self, out_arr, context=None):
if context[0] is np.sin:
new_arr = [np.sin(self.arr[0]), np.cos(self.arr[0])*self.arr[1]]
return MyClass(new_arr)
elif context[0] is np.cos:
new_arr = [np.cos(self.arr[0]), -np.sin(self.arr[0])*self.arr[1]]
return MyClass(new_arr)
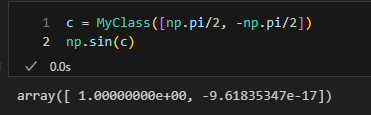
多分、正しいだろう。ちなみに今回使用していないout_arrには、context(self.__array__)したときの結果が返ってくるらしい。__array__wrap__の直後にprint(out_arr, context)をいれたらこうなる。
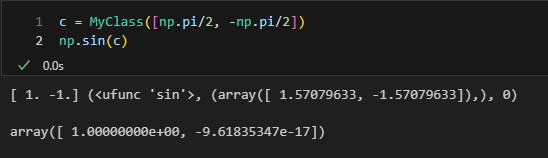
そしたらこんなことも出来るようになる。嬉しいね。
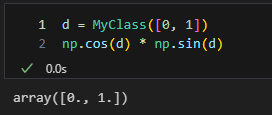
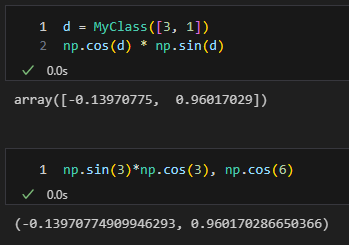
これは\(\sin{x}\cos{x}\)を\(x=0\)付近でテイラー展開すると\(x-2x^3/3+\cdots\)であり、1次の係数は1ですよということを右側の数字が意味しているんだろう。
\(x=3\)の付近でテイラー展開するとこう。Wolfram Alphaと言ってることが同じだ、僕の計算を信じてほしい。

ここで残念なお知らせなのですが、今日みんなと一緒に作成したプログラムは、来週からの内容に適用することはできません。
コメントを投稿
注意事項- 承認を受けるまでコメントは公開されません。
- 非公開を希望した場合、コメントは公開されません。
