2023年12月6日

今日の活動

Spotifyでまとめみたいなのやってたから思い出したかのごとくSpotify聞いてた。1-3月ごろにお気に入り登録してた曲、今聞いてもよいな。過去の自分が偉い。

スープカレー

微分アレルギーの人をこのブログからつなぎとめるための犬。

\([a, b] + [c, d] = [a+b, c+d]\)

\(t \times [a, b] = [ta, tb]\)

\([a, b] \times [c, d] = [ac, ad+bc]\)

\(1/[a, b] = [1/a, -b/a^2] \)

\(\sqrt{[a, b]} = [\sqrt{a}, \frac{b}{2\sqrt{a}}]\)

\(f(x) = \frac{x}{1/x+2}\)という関数について、\(f([2, 1]) = [4/5, 12/25]\)で、4/5はf(2)だけど、12/25は何？って話だった。

とりあえず今までの匂わせの通り、とりあえず、f(x)の微分を行う。紙で解くならこんな感じ？

\(f(x) = \frac{x^2}{1+2x}\)より、

\(f'(x) = \frac{2x}{1+2x} + \frac{-2x^2}{(1+2x)^2} \)

\(= \frac{2x(1+2x) - 2x^2}{(1+2x)^2}\)

\(= \frac{2x(1+x)}{(1+2x)^2}\)

まあすぐに紙と鉛筆は出てこないからiPadを引っ張り出し、そこから計算に数分かかるわ、Wolfram Alphaみたら商の微分公式とかいう忘却の彼方にあった公式が紹介されるわと衰えを感じるわけである。(当時も商の微分公式は難しいからやめておこうと思った気もするが)

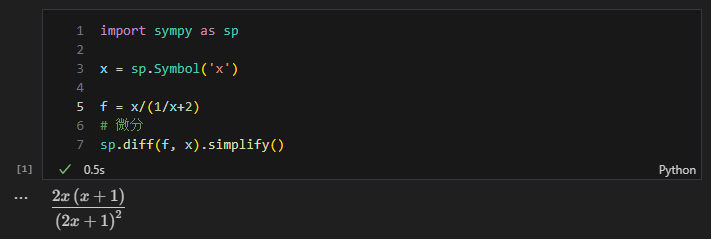
pythonでsympyをインストールできる環境なら下記が早いか。

import sympy as sp

x = sp.Symbol('x')

f = x/(1/x+2)
# 微分
sp.diff(f, x).simplify()

sympy

ちなみに、github copilotを使うと……

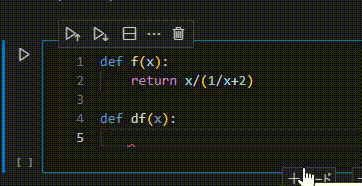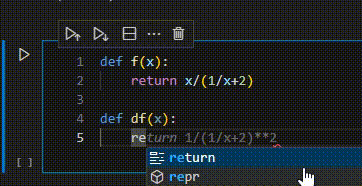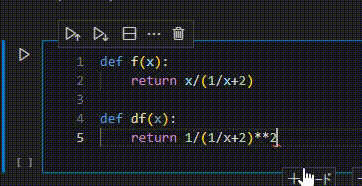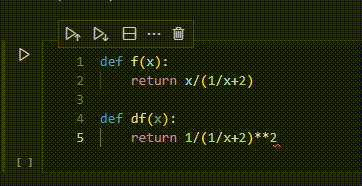
github copilot

うーん。バカ。いやでもいつも使うような関数だとそうでもないんだけどな……、もうちょっとみんなが微分したがりそうな関数とかだとそれっぽいのかな。

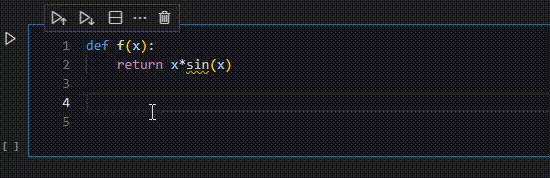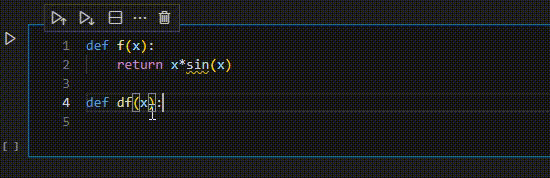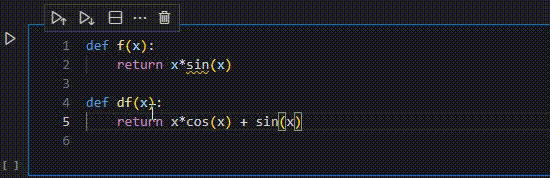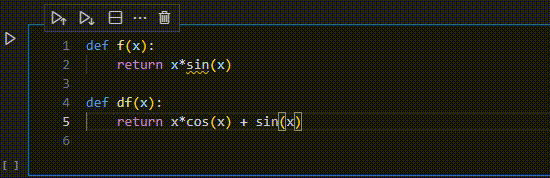
github copilot

話はそれるがgithub copilotで便利なのは、物理定数に強いことだと思う。

github copilot

地球の半径とかちょっとWikipedia数値からずれてる気もするが、おおよそ合ってる。自分が地球の半径の単位わからなくてコメントをつけた瞬間単位を教えてくれるのも楽。

そんなわけで、雑な計算をするヒトにもおすすめできますよという宣伝。なおchatは一度も使い物になった試しがないのでやってない。

微分をするだけで楽しくなってしまった。話を戻すと、\(f'(x) = \frac{2x(1+x)}{(1+2x)^2}\)より\(f'(2) = 12/25\)である。よって、

\(f([2, 1]) = [f(2), f'(2)]\)

となっていたわけである。つまり、今回のような加減乗除で構成されているf(x)に対するf'(2)を求めるだけなら、

\([a, b] \times [c, d] = [ac, ad+bc]\)

\(1/[a, b] = [1/a, -b/a^2] \)

を組み合わせればいい。小学生はともかく、中学生なら解けそうな問題になった。さらに言うと、これならプログラムを自作して微分係数を求められる気がする！って話にもなる。うれしいね。

\(\mathrm{sin}\)関数が自分を仲間にいれてほしいと訴えかけてきているが、FF14のデイリーをやらねばならんので明日以降だ。

< 2023年12月5日 2023年12月7日 >

注意事項